Cytaty
Mikołaja Kopernika

"Spośród licznych i różnorodnych sztuk i nauk, budzących w nas zamiłowanie i będących dla umysłów ludzkich pokarmem, tym – według mego zdania – przede wszystkim poświęcać się należy i te z największym uprawiać zapałem, które obracają się w kręgu rzeczy najpiękniejszych i najbardziej godnych poznania. Takimi są zaś nauki, które zajmują się cudownymi obrotami we wszechświecie i biegami gwiazd, ich rozmiarami i odległościami, ich wschodem i zachodem oraz przyczynami wszystkich innych zjawisk na niebie, a w końcu wyjaśniają cały układ świata. A cóż piękniejszego nad niebo, które przecież ogarnia wszystko, co piękne?"

[Mikołaja Kopernika, „O obrotach. Księga Pierwsza.”, OSSOLINEUM, Towarzystwo Naukowe w Toruniu – Prace Popularnonaukowe nr 50, Wrocław, 1987, str. 19., 9–21 linia]

"Unter den zahlreichen und vielfältigen Künsten und Wissenschaften, die in uns Vorlieben wecken und den menschlichen Geist nähren, sollten wir meiner Meinung nach vor allem denen unsere Aufmerksamkeit widmen und uns mit größtem Eifer mit ihnen beschäftigen, die sich mit den schönsten und am meisten wissenswerten Dingen befassen. Solche Wissenschaften sind diejenigen, die sich mit den wunderbaren Umläufen im Universum und den Bewegungen der Sterne, ihren Größen und Entfernungen, ihrem Auf- und Untergang sowie den Ursachen aller anderen Himmelserscheinungen beschäftigen und schließlich die gesamte Anordnung der Welt erklären. Und was ist schöner als der Himmel, der doch alles Schöne umschließt?"

[Nikolaus Kopernikus, „Über die Umlaufbahnen. Erstes Buch.”, OSSOLINEUM, Wissenschaftliche Gesellschaft in Toruń – Populärwissenschaftliche Arbeiten Nr. 50, Wrocław, 1987, S. 19, Zeilen 9-21]

"Among the many various literary and artistic pursuits which invigorate men’s minds, the strongest affection and utmost zeal should, I think, promote the studies concerned with the most beautiful objects, most deserving to be known. "This is the nature of the discipline which deals with the universe’s divine revolutions, the stars’ motions, sizes, distances, risings and settings, as well as the causes of the other phenomena in the sky, and which, in short, explains its whole appearance. What indeed is more beautiful than heaven, which of course contains all things of beauty?

[Mikołaja Kopernika, „O obrotach. Księga Pierwsza.”, OSSOLINEUM, Towarzystwo Naukowe w Toruniu-Prace Popularnonaukowe nr 50, Wrocław, 1987, strona 19, wiersze 9-21]

"Parmi les nombreux et divers arts et sciences, suscitant en nous la passion et nourrissant les réflexions humaines, à ceux-ci – à mon avis – il convient de se consacrer et de les cultiver avec le plus grand enthousiasme; ceux-là qui tournent autour des choses les plus belles et les plus dignes d'être découvertes. Telles dont les sciences qui traitent des merveilleuses révolutions de l’univers et de la course des étoiles, de leurs tailles et distances, de leur lever et coucher, et des causes de tous les autres phénomènes dans le ciel, et qui expliquent finalement tout le système du monde. Et quoi de plus beau que le ciel, qui par ailleurs englobe tout ce qui est beau ?

[Nicolas Copernic, « Des révolutions. Livre un. », OSSOLINEUM, Société scientifique de Toruń – Ouvrages de vulgarisation scientifique n° 50, Wrocław, 1987, page 19, lignes 9-21]

"Tra le numerose e varie arti e scienze, che destano in noi passione e sono nutrimento per le menti umane, è a quelle – a mio avviso – che principalmente bisogna dedicarsi e coltivare con il massimo zelo, che ruotano intorno alle cose più belle e più degne di conoscenza. Tali sono le scienze che si occupano dei meravigliosi moti dell’universo e delle corse delle stelle, delle loro dimensioni e distanze, del loro sorgere e tramontare e delle cause di tutti gli altri fenomeni celesti, e infine spiegano l’intero ordine del mondo. È cosa c'è di più bello del cielo, che abbraccia tutto ciò che è bello?"

[Mikołaj Kopernik, „De revolutionibus. Liber primus.”, OSSOLINEUM, Societas Scientifica Thorunensis – Opera popularia scientifica Nr. 50, Wratislaviae, 1987, pagina 19, lineae 9-21]

"Choć niezliczone są klęski, wskutek których królestwa, księstwa i rzeczypospolite upadać zwykły, to jednak według mego mniemania, cztery są najsilniejsze: niezgoda, śmiertelność, niepłodność ziemi i spodlenie monety. Pierwsze trzy są tak oczywiste, iż nikt im nie przeczy, jednak czwarta, dotycząca monety, uznawana jest tylko przez nielicznych, i to głębiej zastanawiających się wskutek tego, że oddziaływa na upadek państwa nie od razu i gwałtownie, lecz powoli i skrycie."

[Mikołaj Kopernik, „Sposób bicia monety,” Pracownia Wydawnicza „Elset,” ISBN 798-83-61549-45-1, Olsztyn, 2023, str. 50, wers 1-7]

"Although innumerable are the calamities by which kingdoms, principalities and republics used to fall, but in my opinion, four are the strongest: discord, mortality, the infertility of the earth and the debasement of coinage. The first three are so obvious that no one denies them, however, the fourth, concerning the coinage, is recognised only by a few, and more deeply reflecting on the fact that it has an effect on the decline of the state not immediately and violently, but slowly and secretly."

[Mikołaj Kopernik, „Sposób bicia monety,” Pracownia Wydawnicza „Elset,” ISBN 798-83-61549-45-1, Olsztyn, 2023, str. 50, wers 1-7]

Jednym z najważniejszych odkryć matematycznych Kopernika było twierdzenie sinusów, które obecnie formułuje się następująco:
Dla dowolnego trójkąta ABC wpisanego w okrąg o promieniu R mamy następujące równania:

Twierdzenie Sinusów

Zobacz jak to twierdzenie sformułował Kopernik

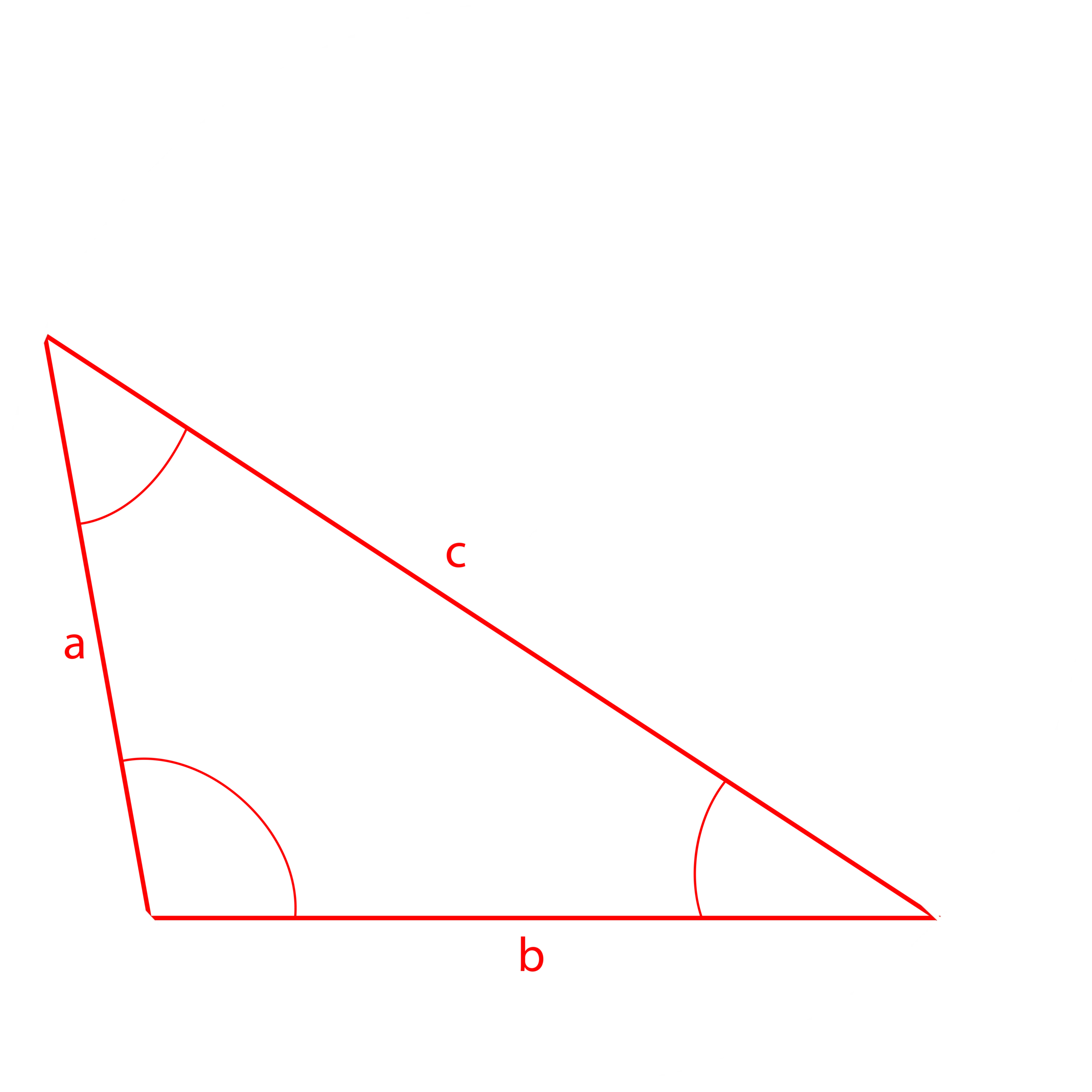
Kopernik rozważył trójkąty wpisane w okrąg o promieniu R formułując następujące twierdzenia:

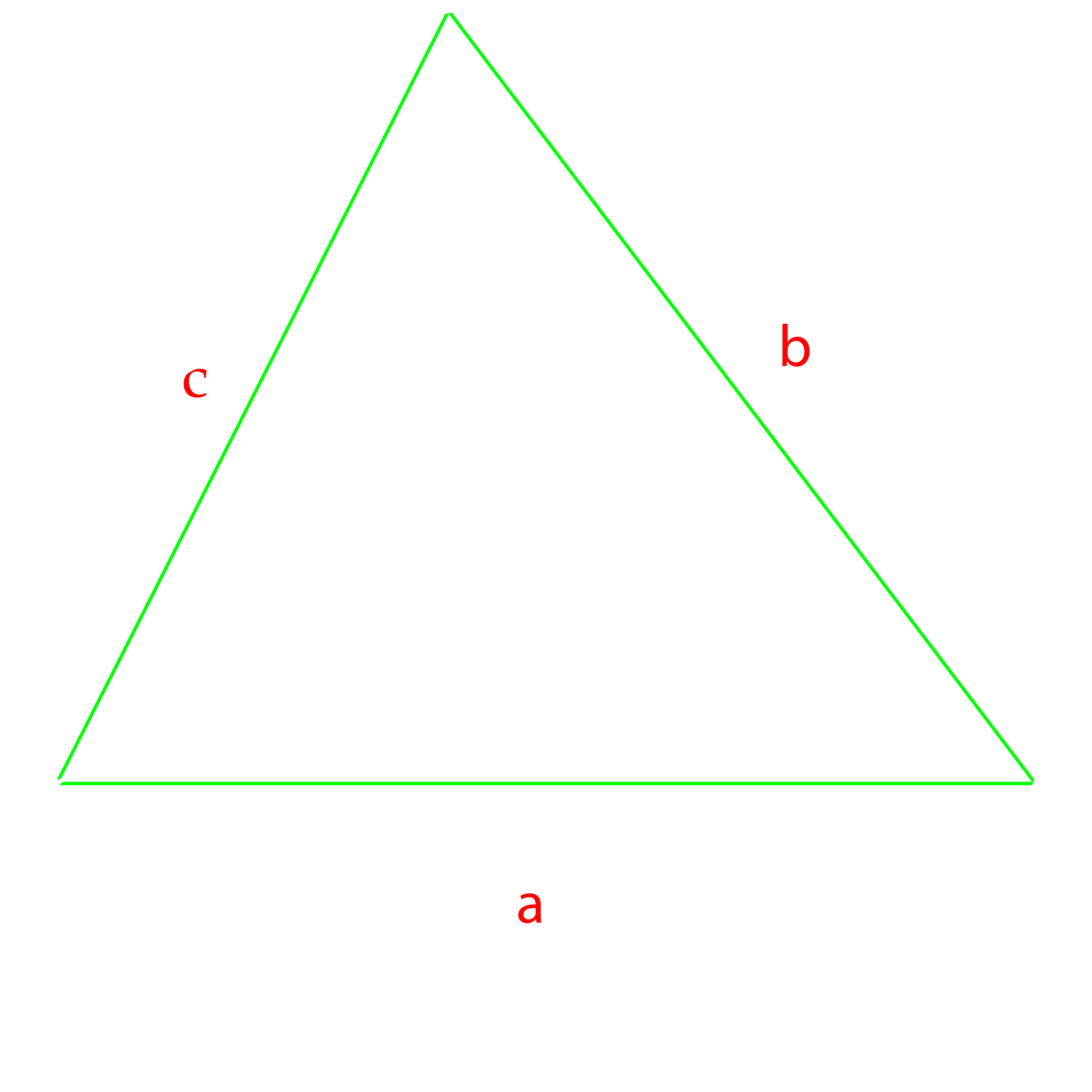
Twierdzenie I.
“W trójkącie gdy wiadome są kąty, wiadome są także stosunki jego boków.”

[Kopernik, Mikołaj (1473-1543), “Mikołaja Kopernika Toruńczyka O obrotach ciał niebieskich ksiąg sześć”, Kujawsko-Pomorska Biblioteka cyfrowa, UMK, 1854, Rozdział XIII, str.57]

Twierdzenie II.
“Jeżeli w trójkącie jeden kąt i dwa boki są dane, trzeci bok i dwa inne katy będą wiadome.”

[Kopernik, Mikołaj (1473-1543), “Mikołaja Kopernika Toruńczyka O obrotach ciał niebieskich ksiąg sześć”, Kujawsko-Pomorska Biblioteka cyfrowa, UMK, 1854, Rozdział XIII, str.57]

Twierdzenie VII.
“Gdy wszystkie boki trójkąta są dane, wiadome będą i jego kąty.”

[Kopernik, Mikołaj (1473-1543), “Mikołaja Kopernika Toruńczyka O obrotach ciał niebieskich ksiąg sześć”, Kujawsko-Pomorska Biblioteka cyfrowa, UMK, 1854, Rozdział XIII, str.60]

Kopernikańskie twierdzenia cosinusów dla trójkątów sferycznych

Rozdział XIV

Twierdzenia III i XII

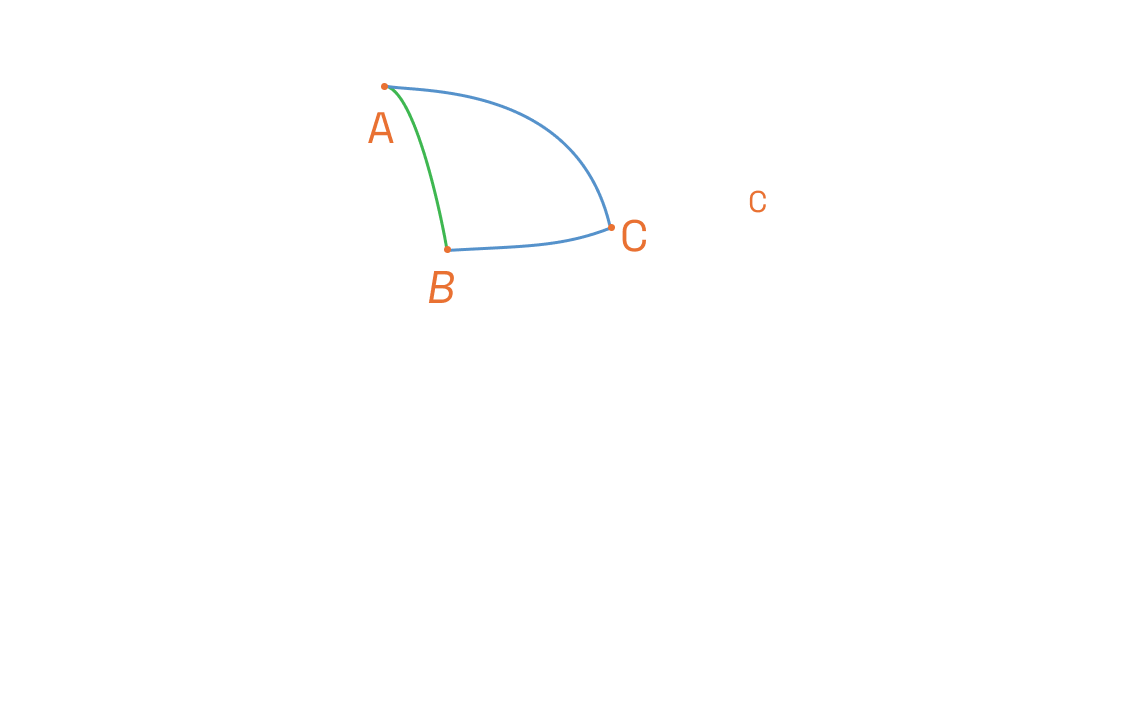
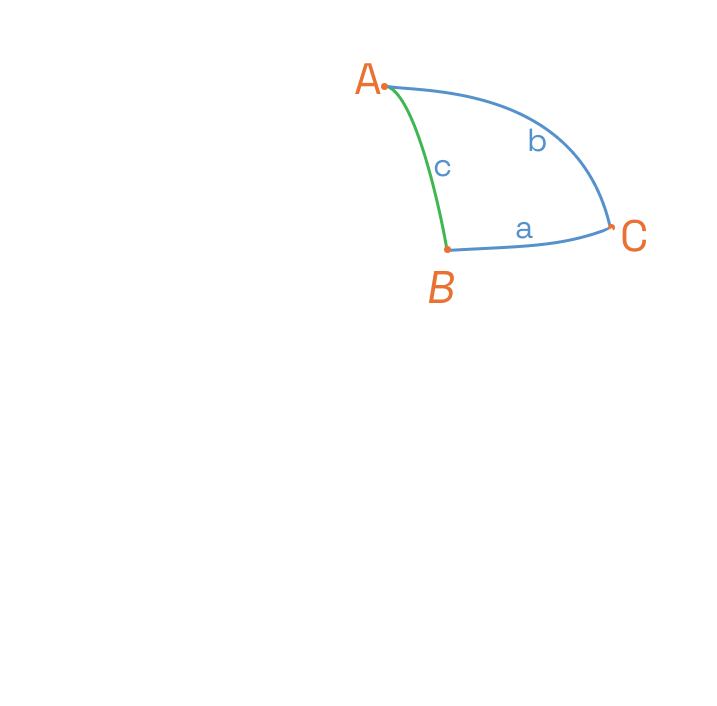
Rozważamy trzy punkty A, B, i C na sferze o promieniu R. Jeżeli połączymy je łukami (wzdłuż kół wielkich) to otrzymamy trójkąt sferyczny ABC.
Rozważamy trójkąty, które są prostokątne i mają boki krótsze niż półokrąg, jak na rysunku.

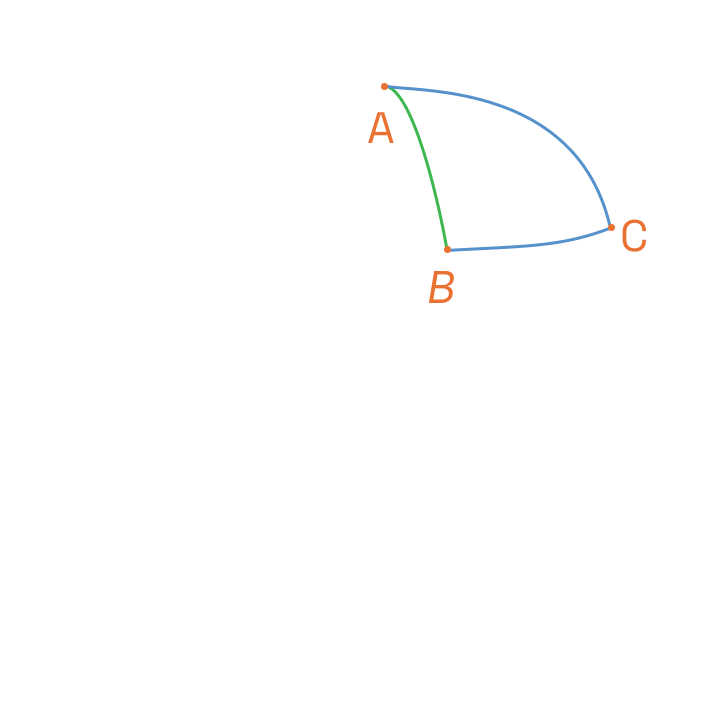
III Twierdzenie Kopernika:

W prostokątnym trójkącie sferycznym ABC na sferze o promieniu R (gdzie kąt C jest prosty) zachodzą następujące proporcje pomiędzy długościami boków:

AB / BC = R / BC

Czyli że stosunek przeciwprostokątnej do jednej z przyprostokątnych jest równy stosunkowi promienia do drugiej przyprostokątnej. Znaczy to, że jeżeli znamy dwa boki, to możemy znaleźć trzeci.

[Kopernik, Mikołaj (1473-1543), “Mikołaja Kopernika Toruńczyka O obrotach ciał niebieskich ksiąg sześć”, Kujawsko-Pomorska Biblioteka cyfrowa, UMK, 1854, Rozdział XIII, str.63-64]

Czyli Kopernik dowiódł szczególną wersję twierdzenia cosinusów dla trójkątów sferycznych. Teraz możemy założyć że promień sfery R =1.

Mierzymy w radianach długość boku (łuku) leżącego naprzeciwko danego kąta jako łuku na sferze (od środka sfery) i mamy:

AB = c BC = a AC = b
(tutaj a, b, c są miarami kątów AOB, BOC, AOC w radianach)

Jeżeli kąt C jest prosty, możemy zapisać twierdzenie Kopernika jako

cos c / cos b = cos a

Twierdzenia Pitagorasa dla trójkątów sferycznych

Znaczy to, że jeżeli znamy dwa boki, to możemy znaleźć trzeci. To jest sferyczna wersja twierdzenia Pitagorasa, które możemy zapisać jako:

cos c = cos b cos a

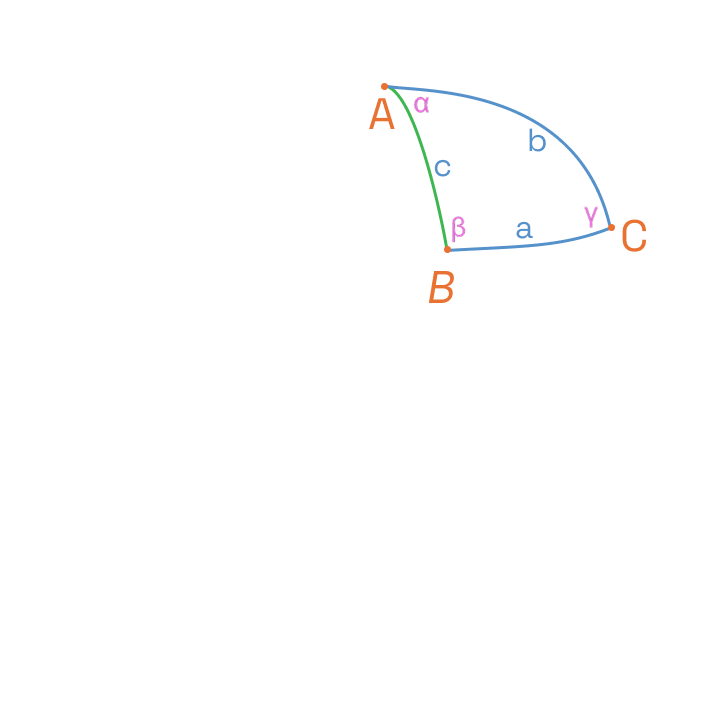
Mamy też ogólniejsze twierdzenie cosinusów dla trójkątów sferycznych na sferze o promieniu R =1, gdzie kąty α, β, γ są kątami sferycznymi trójkąta ABC.

XII Twierdzenie Kopernika:
cos c = cos a cos b + sin a sin b cos γ

Znaczy to, że jeżeli znamy dwa boki i przynajmniej jeden kąt, to możemy znaleźć trzeci, co jest sferyczną wersją twierdzenia cosinusów dla wszystkich trójkątów płaskich.

CytatyMikołaja Kopernika

”Quis enim inhaerdo iis, quae in optimo ordine constituta videat divina dispensation dirigi: assidua eorum contemplation et quadam consuetudine non provocetur ad optima, admireturque Opificem omnium, in quo tota felicitas est et omne bonum?"

Cytaty
Mikołaja Kopernika